Calculating The Surface Area Of A Sphere. Found On Imgur.

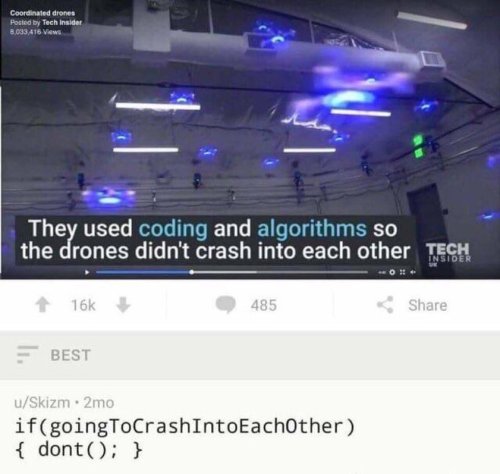
Six stages of debugging

Neutron Stars Are Even Weirder Than We Thought

Let’s face it, it’s hard for rapidly-spinning, crushed cores of dead stars NOT to be weird. But we’re only beginning to understand how truly bizarre these objects — called neutron stars — are.

Neutron stars are the collapsed remains of massive stars that exploded as supernovae. In each explosion, the outer layers of the star are ejected into their surroundings. At the same time, the core collapses, smooshing more than the mass of our Sun into a sphere about as big as the island of Manhattan.

Our Neutron star Interior Composition Explorer (NICER) telescope on the International Space Station is working to discover the nature of neutron stars by studying a specific type, called pulsars. Some recent results from NICER are showing that we might have to update how we think about pulsars!

Here are some things we think we know about neutron stars:

Pulsars are rapidly spinning neutron stars ✔︎

Pulsars get their name because they emit beams of light that we see as flashes. Those beams sweep in and out of our view as the star rotates, like the rays from a lighthouse.

Pulsars can spin ludicrously fast. The fastest known pulsar spins 43,000 times every minute. That’s as fast as blender blades! Our Sun is a bit of a slowpoke compared to that — it takes about a month to spin around once.

The beams come from the poles of their strong magnetic fields ✔︎

Pulsars also have magnetic fields, like the Earth and Sun. But like everything else with pulsars, theirs are super-strength. The magnetic field on a typical pulsar is billions to trillions of times stronger than Earth’s!

Near the magnetic poles, the pulsar’s powerful magnetic field rips charged particles from its surface. Some of these particles follow the magnetic field. They then return to strike the pulsar, heating the surface and causing some of the sweeping beams we see.

The beams come from two hot spots… ❌❓✔︎ 🤷🏽

Think of the Earth’s magnetic field — there are two poles, the North Pole and the South Pole. That’s standard for a magnetic field.

On a pulsar, the spinning magnetic field attracts charged particles to the two poles. That means there should be two hot spots, one at the pulsar’s north magnetic pole and the other at its south magnetic pole.

This is where things start to get weird. Two groups mapped a pulsar, known as J0030, using NICER data. One group found that there were two hot spots, as we might have expected. The other group, though, found that their model worked a little better with three (3!) hot spots. Not two.

… that are circular … ❌❓✔︎ 🤷🏽

The particles that cause the hot spots follow the magnetic field lines to the surface. This means they are concentrated at each of the magnetic poles. We expect the magnetic field to appear nearly the same in any direction when viewed from one of the poles. Such symmetry would produce circular hot spots.

In mapping J0030, one group found that one of the hot spots was circular, as expected. But the second spot may be a crescent. The second team found its three spots worked best as ovals.

… and lie directly across from each other on the pulsar ❌❓✔︎ 🤷🏽

Think back to Earth’s magnetic field again. The two poles are on opposite sides of the Earth from each other. When astronomers first modeled pulsar magnetic fields, they made them similar to Earth’s. That is, the magnetic poles would lie at opposite sides of the pulsar.

Since the hot spots happen where the magnetic poles cross the surface of the pulsar, we would expect the beams of light to come from opposite sides of the pulsar.

But, when those groups mapped J0030, they found another surprising characteristic of the spots. All of the hot spots appear in the southern half of the pulsar, whether there were two or three of them.

This also means that the pulsar’s magnetic field is more complicated than our initial models!

J0030 is the first pulsar where we’ve mapped details of the heated regions on its surface. Will others have similarly bizarre-looking hotspots? Will they bring even more surprises? We’ll have to stay tuned to NICER find out!

And check out the video below for more about how this measurement was done.

Make sure to follow us on Tumblr for your regular dose of space: http://nasa.tumblr.com.

How is geometry entangled in the fabric of the Universe?

Geometry can be seen in action in all scales of the Universe, be it astronomical – in the orbital resonance of the planets for example, be it at molecular levels, in how crystals take their perfect structures. But going deeper and deeper into the fabric of the material world, we find that at quantum scale, geometry is a catalyst for many of the laws of quantum-physics and even definitions of reality.

Take for example the research made by Duncan Haldane, John Michael Kosterlitz and David Thouless, the winners of the 2016 Nobel prize in physics. By using geometry and topology they understood how exotic forms of matter take shape based on the effects of the quantum mechanics. Using techniques borrowed from geometry and topology, they studied the changes between states of matter (from plasma to gas, from gas to liquid and from liquid to solid) being able to generate a set of rules that explain different types of properties and behaviors of matter. Furthermore, by coming across a new type of symmetry patterns in quantum states that can influence those behaviors or even create new exotic types of matter, they provided new meaning and chance in using geometry as a study of “the real”.

If the Nobel Prize winners used abstract features of geometry to define physical aspects of matter, more tangible properties of geometry can be used to define other less tangible aspects of reality, like time or causality. In relativity, 3d space and 1d time become a single 4d entity called “space-time”, a dimension perceived through the eye of a space-time traveler. When an infinite number of travelers are brought into the equation, the numbers are adding up fast and, to see how for example, a space-time of a traveler looks for another traveler,  we can use geometric diagrams of these equations. By tracing what a traveler “sees” in the space-time dimension  and assuming that we all see the same speed of light, the intersection points of view between a stationary traveler and a moving one give a hyperbola that represents specific locations of space-time events seen by both travelers, no matter of their reference frame. These intersections represent a single value for the space-time interval, proving that the space-time dimension is dependent of the geometry given by the causality hyperbola.

If the abstract influence of geometry on the dimensions of reality isn’t enough,  take for example one of the most interesting experiments of quantum-physics, the double-split experiment, were wave and particle functions are simultaneously proven to be active in light or matter. When a stream of photons is sent through a slit against a wall, the main expectation is that each photon will strike the wall in a straight line. Instead, the photons are rearranged by a specific type of patterns, called diffraction patterns, a behavior mostly visible for small particles like electrons, neutrons, atoms and small molecules, because of their short wavelength.

Two slits diffraction pattern by a plane wave. Animation by Fu-Kwun Hwang 

The wave-particle duality is a handful, since it is a theory that has worked well in physics but with its meaning or representation never been satisfactorily resolved. Perhaps future experiments that will involve more abstract roles of geometry in quantum fields, like in the case of the Nobel prize winners, will develop new answers to how everything functions at these small scales of matter.

In this direction, Garret Lissi tries to explain how everything works, especially at quantum levels, by uniting all the forces of the Universe, its fibers and particles, into a 8 dimensions geometric structure. He suggests that each dot, or reference, in space-time has a shape, called fibre, attributed to each type of particle. Thus, a separate layer of space is created, parallel to the one we can perceive, given by these shapes and their interactions. Although the theory received also good reviews but also a widespread skepticism, its attempt to describe all known fundamental aspects of physics into one possible theory of everything is laudable. And proving that with laws and theories of geometry is one step closer to a Universal Geometry theory.

gotta catch em all

Interesting submission rk1232! Thanks for the heads up! :D :D

I got a migraine and threw up because of this

Note to self: debugging

always remember to remove the Log.d(”Well fuck you too”) lines and the variables named “wtf” and “whhhyyyyyyy” before pushing anything to git

Everyone who reblogs this will get a pick-me-up in their ask box.

Every. Single. One. Of. You.