The 21 Card Trick Created In Python.

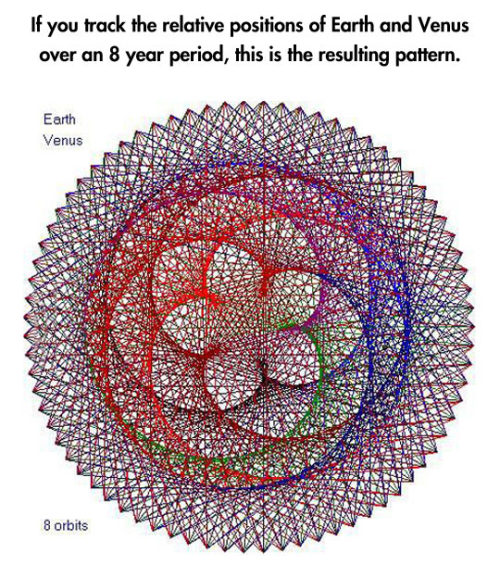
Planetary Frequencies.

People think coding / debugging means highly concentrated furious typing, but mostly it’s just angrily staring at the screen for long periods of time waiting for the problem to solve itself

Raspberry Multiverse

Stephen Hawking’s Grand design is leading to a non symmetric multiverse. However there is reason to suggest a full symmetric multiverse with point symmetry at the centre of a raspberry shaped pulsating bubble multiverse. For an entangled multiverse, each quantum should have its own 12 fold entanglement relation to all 12 opposite (anti) quantums, each located inside one of the 12 universes. The result is called: Poincaré dodecahedral space symmetry.  (see also below: B.F.Roukema) A dodecahedron is also called “Buckyball” An other evidence for space symmetry and the centre of the multiverse is the so called DARK FLOW. Dark flow seems to be found at the edge of the visible universe!! There the “dark flow centre is represented by a so called "Pitch of spacetime”

The Kakeya Problem

Some time ago I (briefly) mentioned that, along with two other students, I was taking a reading course this semester with Dmitriy Bilyk. It hasn’t quite gone in the direction we were initially expecting, but one of our long detours has been an extended sequence of readings around the the Kakeya conjecture. As far as I know, the Kakeya problem (different from the Kakeya conjecture; more on that later) was the first question that fell respectably under the purview of geometric measure theory. So if nothing else, it is interesting from a historical perspective as a question that kickstarted a whole new field of mathematics.

Okay, but what is the Kakeya problem?

As originally posed, it goes like this: given a disk with diameter 1, it is possible to place down a line segment of length 1 into the set, and rotate it (continuously) an entire 180 degrees. But this is not the smallest-area set for which this kind of rotation is possible:

(all pictures in the post are from the Wikipedia page, which is really good)

This set has area $\tau/16$, half that of the circle. So the question naturally becomes: what is the area of the smallest set that allows this kind of rotation?

The answer is known, and it is…

…

zero, basically.

It’s remarkable, but it’s true: you can construct arbitrarily small sets in which you can perform a 180-degree rotation of a line segment! One way to do it goes like this: in the picture above, we reduced the area of the circle by squeezing it until it developed three points. If we keep squeezing to get more points, then the solid “middle” becomes very small, and the tendrils get very thin, so the area keeps decreasing. However, we can still take a line segment and slowly, methodically, shift it back and forth between the set’s pointy bits, parallel-parking style, to eventually get the entire 180 degrees of rotation.

——

You can’t actually get a set with zero area to work. But the reason for that seemed more like a technicality than something actually substantial. So people changed the problem slightly to get rid of those concerns. Now, instead of trying to get a set where you can rotate a line segment through all 180 degrees, you just have to have a set where you can find a line segment in every direction. The difference being that you don’t need to guarantee any smooth way to “move between” these line segments.

Sets that work for the modified problem are often called Kakeya sets (although some people reserve that for the rotation problem and use Besicovitch sets for the modified one). And indeed, there are Kakeya sets which actually have zero area.

The details involved with going from “arbitrarily small” to “actually zero” are considerable, and we won’t get into them here. The following is a simplification (due to Perron) of Besicovitch’s original construction for the “arbitrarily small” case. We take a triangle which clearly has ½ of the directions the needle might possibly take, and split it up into several pieces in such a way that no directions are lost. Then we start to overlap those pieces to get a set (that still has segments in all the same directions) with much smaller area:

We can do this type of construction twice (one triangle “downward-facing” and the other “left-facing”) and then put those two sets together, guarantee that we get all of 180 degrees of directions.

This Besicovitch-Perron construction, itself, only produces sets which are “arbitrarily small”, but was later refined to go all the way to zero. Again, the technicalities involved in closing that gap are (much) more than I want to talk about now. But the fact that these technicalities can be carried out with the Besicovitch-Perron construction is what makes it “better” than the usual constructions for the original Kakeya problem.

——

I should conclude with a few words about the Kakeya conjecture, since I promised them earlier :)

Despite the essentially-solved status of these two classical Kakeya problems, there is at least one big question still left open. It is rather more technical than the original ones, and so doesn’t get a lot of same attention, but I’d like to take a stab at explaining what’s still current research in this sphere of ideas.

Despite the fact that Kakeya sets can be made to be “small” in the sense of measure, we still intuitively want to believe these sets are “big”. There are many ways we can formalize largeness of sets (in $\Bbb R^n$, in particular) but the one that seems to be most interesting for Kakeya things is the notion of Hausdorff dimension. I won’t define the term here, but if you’ve ever heard someone spouting off about fractals, you’ve probably heard the phrase “Fractals have non-integer dimension!”. This is the notion of dimension they’re talking about.

It is known that Kakeya sets in the plane have Hausdorff dimension 2, and that in general a Kakeya set in $n>2$ dimensions has Hausdorff dimension at least $\frac{n}{2}+1$. The proofs of these statements are… difficult, and the general case remains elusive.

One thing more: you can also formulate the Kakeya conjecture in finite fields: in this setting having “dimension $n$” in a vector space over the field $\Bbb F_q$ means that you have a constant times $q^n$ number of points in your set. Wolff proposed this “technicality-free” version in 1999 as a way to study the conjecture for $\Bbb R$. And indeed, a lot of the best ideas for the problem in $\Bbb R$ have come from doing some harmonic analysis on the ideas originally generated for the finite field case. 

But then in 2008 Zeev Dvir went and solved the finite field case completely. Which on one hand is great! But on the other hand, Dvir’s method definitely can’t be finessed to work in $\Bbb R$ so we still have work to do :P

——

Partially I wanted to write about this because it’s cool in its own right, but I must admit that my main motivation is a little more pragmatic. There was a talk at SEICCGTC 2017 which showed a surprising connection between the Kakeya problem and a certain combinatorial game. So if you think these ideas are at all interesting, you may enjoy reading the next two posts in this sequence about that talk.

[ Post 1 ] [ Next ]

How to draw a regular pentagon [x]

When 25,000 little dice are agitated in a cylinder, they form into neat concentric circles

Behold the magic of compaction dynamics. Scientists from Mexico and Spain dumped 25,000 tiny dice (0.2 inches) into a large clear plastic cylinder and rotated the cylinder back and forth once a second. The dice arranged themselves into rows of concentric circles. See the paper and the videos here.

https://boingboing.net/2017/12/05/when-25000-little-dice-are-ag.html

Hey guys, I’m observing a high school class and was looking at a textbook, and learned that irrationals are closed under addition! Super cool, who knew!

Speaking of pretty flowers, may I present to you the “Eighteen Scholars”, the flower of my heart-a variation of Camellia japonica L. Its uniqueness lies in the layers and layers of petals-one flower can hold as much as 130 petals.

Named “Eighteen Scholars” in Chinese because at the most, one bush can have up to eighteen of these pretty darlings :3

We Need Your Help to Find STEVE

Glowing in mostly purple and green colors, a newly discovered celestial phenomenon is sparking the interest of scientists, photographers and astronauts. The display was initially discovered by a group of citizen scientists who took pictures of the unusual lights and playfully named them “Steve.”

When scientists got involved and learned more about these purples and greens, they wanted to keep the name as an homage to its initial name and citizen science discoverers. Now it is STEVE, short for Strong Thermal Emission Velocity Enhancement.

Credit: ©Megan Hoffman

STEVE occurs closer to the equator than where most aurora appear – for example, Southern Canada – in areas known as the sub-auroral zone. Because auroral activity in this zone is not well researched, studying STEVE will help scientists learn about the chemical and physical processes going on there. This helps us paint a better picture of how Earth’s magnetic fields function and interact with charged particles in space. Ultimately, scientists can use this information to better understand the space weather near Earth, which can interfere with satellites and communications signals.

Want to become a citizen scientist and help us learn more about STEVE? You can submit your photos to a citizen science project called Aurorasaurus, funded by NASA and the National Science Foundation. Aurorasaurus tracks appearances of auroras – and now STEVE – around the world through reports and photographs submitted via a mobile app and on aurorasaurus.org.

Here are six tips from what we have learned so far to help you spot STEVE:

1. STEVE is a very narrow arc, aligned East-West, and extends for hundreds or thousands of miles.

Credit: ©Megan Hoffman 

2. STEVE mostly emits light in purple hues. Sometimes the phenomenon is accompanied by a short-lived, rapidly evolving green picket fence structure (example below).

Credit: ©Megan Hoffman 

3. STEVE can last 20 minutes to an hour.

4. STEVE appears closer to the equator than where normal – often green – auroras appear. It appears approximately 5-10° further south in the Northern hemisphere. This means it could appear overhead at latitudes similar to Calgary, Canada. The phenomenon has been reported from the United Kingdom, Canada, Alaska, northern US states, and New Zealand.

5. STEVE has only been spotted so far in the presence of an aurora (but auroras often occur without STEVE). Scientists are investigating to learn more about how the two phenomena are connected. 

6. STEVE may only appear in certain seasons. It was not observed from October 2016 to February 2017. It also was not seen from October 2017 to February 2018.

Credit: ©Megan Hoffman 

STEVE (and aurora) sightings can be reported at www.aurorasaurus.org or with the Aurorasaurus free mobile apps on Android and iOS. Anyone can sign up, receive alerts, and submit reports for free.

Make sure to follow us on Tumblr for your regular dose of space: http://nasa.tumblr.com.