matematicaulysses

Latest Posts by matematicaulysses

Just Descending

Can’t find the creator of this. I saw it tweeted by Alexander Bogomolny. It’s Escher, of course, but also the Penrose staircase. Roger and his father! Great #mathart story. See Wikipedia for more.

Plate 17. Guide to the construction of Gothic details. 1888.

Internet Archive

Of course Saturn brought its ring light.

On June 25, 2023, our James Webb Space Telescope made its first near-infrared observations of Saturn. The planet itself appears extremely dark at this infrared wavelength, since methane gas absorbs almost all the sunlight falling on the atmosphere. The icy rings, however, stay relatively bright, leading to Saturn’s unusual appearance in this image.

This new image of Saturn clearly shows details within the planet’s ring system, several of the planet’s moons (Dione, Enceladus, and Tethys), and even Saturn’s atmosphere in surprising and unexpected detail.

These observations from Webb are just a hint at what this observatory will add to Saturn’s story in the coming years as the science team delves deep into the data to prepare peer-reviewed results.

Download the full-resolution image, both labeled and unlabeled, from the Space Telescope Science Institute.

Make sure to follow us on Tumblr for your regular dose of space!

Robert Mangold - Compound Ring Study (2011)

Agnes Denes. Isometric Systems in Isotropic Space: The Pyramid, 1976

Mel Bochner, Untitled (“Child’s Play!”: ‘Study for 7-Part Progression’), (pen and black ink on off-white wove paper), 1966 [Art Institute Chicago, Chicago, IL. © Mel Bochner]

Did you know that there is a way of cutting an equilateral triangle into seven similar triangles that have pairwise different sizes, and they are not right triangles? (With right triangles it is easy to cut into any number of similar pieces.)

One of the angles in each triangle is 120 degrees and the other two are roughly 40.67915375798 and 19.32084624 degrees. You can read the details in the paper:

A note on perfect dissections of an equilateral triangle by Andrzej Zak

Specimens of Fancy Turning

Public Domain Review covered this 19th century book of some pretty great spirograph images.

M. C. Escher - Metamorphose II

More on the Spectre

Images from this great Yoshiaki Araki thread. (If you're interested in tessellations and are twitterpated, he's a must follow.)

He links the Nature article (good and a free read).

Best one, so far:

Robert Farthauer suggests:

And, of course, the actual article, by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss.

Kaplan gives this illustration of the tile:

He has a one page stop for info about the tiling.

Bonus: via New-Cleckit Dominie

Hokusai Part II

David Bailey shared the link to this book full of classical Japanese artist Hokusai's sketches on tessellations. Awesome. Too awesome for one post, and together they're less than half the book!

Shearer’s geometry puzzles

On his blog MathWithBadDrawings, Ben Orlin reposted a couple of geometrical sangaku-like puzzles by math teacher Catriona Shearer. These are eleven of her personal favorites. If you dare, definitely give them a try!

Transit Across a Purple Sun. What’s the total shaded area?

Shearer’s Emerald. Four squares. What’s the shaded area?

The Pyramid with Two Tombs. Two squares inside an equilateral triangle. What’s the angle?

Setting Sun, Rising Moon. What fraction of the rectangle is shaded?

Hex Hex Six. Both hexagons are regular. How long is the pink line?

Four, Three, Two. What’s the area of this triangle?

The Trinity Quartet. All four triangles are equilateral. What fraction of the rectangle do they cover?

The Falling Domino. This design is made of three 2×1 rectangles. What fraction of it is shaded?

Slices in a Sector. The three colored sections here have the same area. What’s the total area of the square?

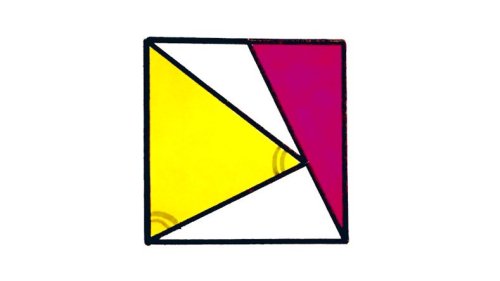
Disorientation. The right-angled triangle covers ¼ of the square. What fraction does the isosceles triangle cover?

Sunny Smile Up. What fraction of the circle is shaded?

Gego: Measuring Infinity

New MOMA exhibit. Via Joanne Growney.

saurez vous répondre sur cette question ? #Olympiad #france

Luiz Sacilotto [Brazil] (1924-2003) ~ ‘C8752’, 1987. Acrylic and watercolor on canvas (89,9 x 89,9 cm).

Via Ann Bingham.

Que representação fantástica!

Aaahh, mucho más claro...

Project Euler has this problem called Laserbeam. It starts as one thing but leads somewhere completely different.

Cool !

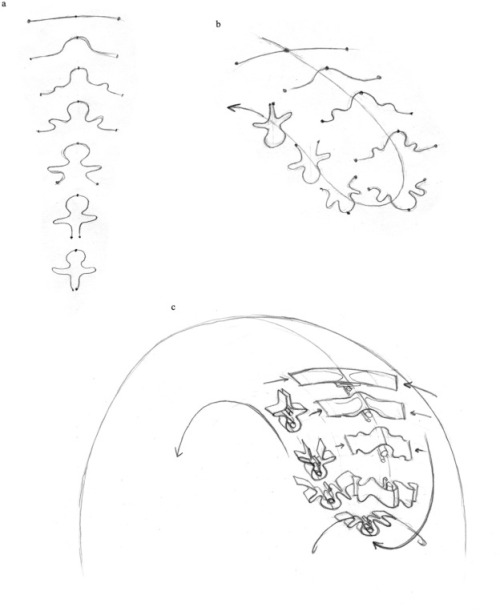
Embryo geometry: a theory of evolution from a single cell to the complex vertebrate body

24 “blueprints” that illustrate how the musculoskeletal, cardiovascular, neurological, and reproductive systems evolve through the mechanical deformation of geometric patterns. These images show how the vertebrate body might have evolved from a single cell during the evolutionary time and during individual development.

Though neither rigorous nor exhaustive in an empirical sense, our model offers an intuitive and plausible description of the emergence of form via simple geometrical and mechanical forces and constraints. The model provides a template, or roadmap, for further investigation, subject to confirmation (or refutation) by interested researchers.

The concept of “embryo geometry” suggests that the vertebrate embryo might be produced by mechanical deformation of the blastula, a ball of cells formed when a fertilized egg splits. As these cells multiply, the volume and surface area of the ball expand, changing its shape. According to the hypothesis, the blastula preserves the geometry of the initial eight cells generated by the egg’s first three divisions, which establish the three axes of the vertebrate body.

Though speculative, the model addresses the poignant absence in the literature of any plausible account of the origin of vertebrate morphology. A robust solution to the problem of morphogenesis—currently an elusive goal—will only emerge from consideration of both top-down (e.g., the mechanical constraints and geometric properties considered here) and bottom-up (e.g., molecular and mechano-chemical) influences.

Origin of the vertebrate body plan via mechanically biased conservation of regular geometrical patterns in the structure of the blastula, David B. Edelman, Mark McMenamin, Peter Sheesley, Stuart Pivar

Published: September 2016, Progress in Biophysics and Molecular Biology DOI: 10.1016/j.pbiomolbio.2016.06.007