There Are 27 Straight Lines On A Smooth Cubic Surface (always; For Real!)
There are 27 straight lines on a smooth cubic surface (always; for real!)
This talk was given by Theodosios Douvropoulos at our junior colloquium.
I always enjoy myself at Theo’s talks, but he has picked up Vic’s annoying habit of giving talks that are nearly impossible to take good notes on. This talk was at least somewhat elementary, which means that I could at least follow it while being completely unsure of what to write down ;)
——
A cubic surface is a two-dimensional surface in three dimensions which is defined by a cubic polynomial. This statement has to be qualified somewhat if you want to do work with these objects, but for the purpose of listening to a talk, this is all you really need.
The amazing theorem about smooth cubic surfaces was proven by Arthur Cayley in 1849, which is that they contain 27 lines. To be clear, “line” in this context means an actual honest-to-god straight line, and by “contain” we mean that the entire line sits inside the surface, like yes all of it, infinitely far in both directions, without distorting it at all.

(source)
[ Okay, fine, you have to make some concession here: the field has to be algebraically closed and the line is supposed to be a line over that field. And $\Bbb R$ is not algebraically closed, so a ‘line’ really means a complex line, but that’s not any less amazing because it’s still an honest, straight, line. ]
This theorem is completely unreasonable for three reasons. First of all, the fact that any cubic surface contains any (entire) lines at all is kind of stunning. Second, the fact that the number of lines that it contains is finite is it’s own kind of cray. And finally, every single cubic surface has the SAME NUMBER of lines?? Yes! always; for real!
All of these miracles have justifications, and most of them are kind of technical. Theo spent a considerable amount of time talking about the second one, but after scribbling on my notes for the better part of an hour, I can’t make heads or tails of them. So instead I’m going to talk about blowups.
I mentioned blowups in the fifth post of the sequence on Schubert varieties, and I dealt with it fairly informally there, but Theo suggested a more formal but still fairly intuitive way of understanding blowups at a point. The idea is that we are trying to replace the point with a collection of points, one for each unit tangent vector at the original point. In particular, a point on any smooth surface has a blowup that looks like a line, and hence the blowup in a neighborhood of the point looks like this:

(source)
Here is another amazing fact about cubic surfaces: all of them can be realized as a plane— just an ordinary, flat (complex) 2D plane— which has been blown up at exactly six points. These points have to be “sufficiently generic”; much like in the crescent configuration situation, you need that no two points lie on the same line, and the six points do not all lie on a conic curve (a polynomial of degree 2).
In fact, it’s possible, using this description to very easily recover 21 of the 27 lines. Six of the lines come from the blowups themselves, since points blow up into lines. Another fifteen of them come from the lines between any two locations of blowup. This requires a little bit of work: you can see in the picture that the “horizontal directions” of the blowup are locally honest lines. Although most of these will become distorted near the other blowups, precisely one will not: the height corresponding to the tangent vector pointing directly at the other blowup point.
The remaining six points are can also be understood from this picture: they come from the image of the conic passing through five of the blowup points. I have not seen a convincing elementary reason why this should be true; the standard proof is via a Chow ring computation. If you know anything about Chow rings, you know that I am not about to repeat that computation right here.
This description is nice because it not only tells us how many lines there are, but also it roughly tells us how the lines intersect each other. I say “roughly” because you do have to know a little more about what’s going on with those conics a little more precisely. In particular, it is possible for three lines on a cubic surface to intersect at a single point, but this does not always happen.
I’ll conclude in the same way that Theo did, with a rushed comment about the fact that “27 lines on a cubic” is one part of a collection of relations and conjectured relations that Arnold called the trinities. Some of these trinities are more… shall we say… substantiated than others… but in any case, the whole mess is Laglandsian in scope and unlikely even to be stated rigorously, much less settled, in our lifetimes. But it makes for interesting reading and good fodder for idle speculation :)
More Posts from Jupyterjones and Others



Fibonacci Sculptures - Part II
These are 3-D printed sculptures designed to animate when spun under a strobe light. The placement of the appendages is determined by the same method nature uses in pinecones and sunflowers. The rotation speed is synchronized to the strobe so that one flash occurs every time the sculpture turns 137.5º—the golden angle. If you count the number of spirals on any of these sculptures you will find that they are always Fibonacci numbers.
© John Edmark

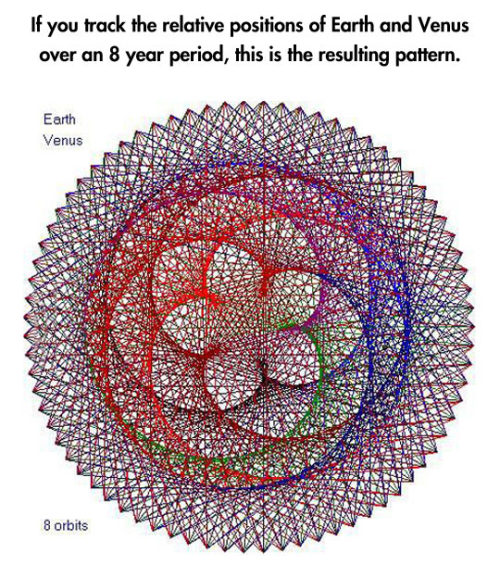
Planetary Frequencies.

That’s the secret of programming.

Programmer LoGiC
Cassini Spacecraft: Top Discoveries
Our Cassini spacecraft has been exploring Saturn, its stunning rings and its strange and beautiful moons for more than a decade.

Having expended almost every bit of the rocket propellant it carried to Saturn, operators are deliberately plunging Cassini into the planet to ensure Saturn’s moons will remain pristine for future exploration – in particular, the ice-covered, ocean-bearing moon Enceladus, but also Titan, with its intriguing pre-biotic chemistry.
Let’s take a look back at some of Cassini’s top discoveries:
Titan

Under its shroud of haze, Saturn’s planet-sized moon Titan hides dunes, mountains of water ice and rivers and seas of liquid methane. Of the hundreds of moons in our solar system, Titan is the only one with a dense atmosphere and large liquid reservoirs on its surface, making it in some ways more like a terrestrial planet.

Both Earth and Titan have nitrogen-dominated atmospheres – over 95% nitrogen in Titan’s case. However, unlike Earth, Titan has very little oxygen; the rest of the atmosphere is mostly methane and traced amounts of other gases, including ethane.

There are three large seas, all located close to the moon’s north pole, surrounded by numerous smaller lakes in the northern hemisphere. Just one large lake has been found in the southern hemisphere.
Enceladus

The moon Enceladus conceals a global ocean of salty liquid water beneath its icy surface. Some of that water even shoots out into space, creating an immense plume!

For decades, scientists didn’t know why Enceladus was the brightest world in the solar system, or how it related to Saturn’s E ring. Cassini found that both the fresh coating on its surface, and icy material in the E ring originate from vents connected to a global subsurface saltwater ocean that might host hydrothermal vents.

With its global ocean, unique chemistry and internal heat, Enceladus has become a promising lead in our search for worlds where life could exist.
Iapetus

Saturn’s two-toned moon Iapetus gets its odd coloring from reddish dust in its orbital path that is swept up and lands on the leading face of the moon.

The most unique, and perhaps most remarkable feature discovered on Iapetus in Cassini images is a topographic ridge that coincides almost exactly with the geographic equator. The physical origin of the ridge has yet to be explained…

It is not yet year whether the ridge is a mountain belt that has folded upward, or an extensional crack in the surface through which material from inside Iapetus erupted onto the surface and accumulated locally.
Saturn’s Rings

Saturn’s rings are made of countless particles of ice and dust, which Saturn’s moons push and tug, creating gaps and waves.

Scientists have never before studied the size, temperature, composition and distribution of Saturn’s rings from Saturn obit. Cassini has captured extraordinary ring-moon interactions, observed the lowest ring-temperature ever recorded at Saturn, discovered that the moon Enceladus is the source for Saturn’s E ring, and viewed the rings at equinox when sunlight strikes the rings edge-on, revealing never-before-seen ring features and details.

Cassini also studied features in Saturn’s rings called “spokes,” which can be longer than the diameter of Earth. Scientists think they’re made of thin icy particles that are lifted by an electrostatic charge and only last a few hours.
Auroras

The powerful magnetic field that permeates Saturn is strange because it lines up with the planet’s poles. But just like Earth’s field, it all creates shimmering auroras.

Auroras on Saturn occur in a process similar to Earth’s northern and southern lights. Particles from the solar wind are channeled by Saturn’s magnetic field toward the planet’s poles, where they interact with electrically charged gas (plasma) in the upper atmosphere and emit light.
Turbulent Atmosphere

Saturn’s turbulent atmosphere churns with immense storms and a striking, six-sided jet stream near its north pole.

Saturn’s north and south poles are also each beautifully (and violently) decorated by a colossal swirling storm. Cassini got an up-close look at the north polar storm and scientists found that the storm’s eye was about 50 times wider than an Earth hurricane’s eye.

Unlike the Earth hurricanes that are driven by warm ocean waters, Saturn’s polar vortexes aren’t actually hurricanes. They’re hurricane-like though, and even contain lightning. Cassini’s instruments have ‘heard’ lightning ever since entering Saturn orbit in 2004, in the form of radio waves. But it wasn’t until 2009 that Cassini’s cameras captured images of Saturnian lighting for the first time.

Cassini scientists assembled a short video of it, the first video of lightning discharging on a planet other than Earth.

Cassini’s adventure will end soon because it’s almost out of fuel. So to avoid possibly ever contaminating moons like Enceladus or Titan, on Sept. 15 it will intentionally dive into Saturn’s atmosphere.

The spacecraft is expected to lose radio contact with Earth within about one to two minutes after beginning its decent into Saturn’s upper atmosphere. But on the way down, before contact is lost, eight of Cassini’s 12 science instruments will be operating! More details on the spacecraft’s final decent can be found HERE.
Make sure to follow us on Tumblr for your regular dose of space: http://nasa.tumblr.com

-
 jupyterjones reblogged this · 6 years ago
jupyterjones reblogged this · 6 years ago -
 mathandmountains liked this · 6 years ago
mathandmountains liked this · 6 years ago -
 dubiousspectrum reblogged this · 6 years ago
dubiousspectrum reblogged this · 6 years ago -
 adelynas liked this · 7 years ago
adelynas liked this · 7 years ago -
 saladfrosting2 reblogged this · 7 years ago
saladfrosting2 reblogged this · 7 years ago -
 risingape reblogged this · 7 years ago
risingape reblogged this · 7 years ago -
 skeletontemple liked this · 7 years ago
skeletontemple liked this · 7 years ago -
 highpriestmckickass reblogged this · 7 years ago
highpriestmckickass reblogged this · 7 years ago -
 thirteen-jades liked this · 7 years ago
thirteen-jades liked this · 7 years ago -
 thirteen-jades reblogged this · 7 years ago
thirteen-jades reblogged this · 7 years ago -
 pencels liked this · 7 years ago
pencels liked this · 7 years ago -
 recursiverecursion liked this · 7 years ago
recursiverecursion liked this · 7 years ago -
 silver-and-ivory liked this · 7 years ago
silver-and-ivory liked this · 7 years ago -
 cromulentenough liked this · 7 years ago
cromulentenough liked this · 7 years ago -
 cromulentenough reblogged this · 7 years ago
cromulentenough reblogged this · 7 years ago -
 syntaxcoloring liked this · 7 years ago
syntaxcoloring liked this · 7 years ago -
 compiler-errors reblogged this · 7 years ago
compiler-errors reblogged this · 7 years ago -
 whereismyphoenix liked this · 7 years ago
whereismyphoenix liked this · 7 years ago -
 girlfriendsofthegalaxy liked this · 7 years ago
girlfriendsofthegalaxy liked this · 7 years ago -
 sufficientlylargen liked this · 7 years ago
sufficientlylargen liked this · 7 years ago -
 yeet-tu-brute liked this · 7 years ago
yeet-tu-brute liked this · 7 years ago -
 beethoventhedragon reblogged this · 7 years ago
beethoventhedragon reblogged this · 7 years ago -
 beethoventhedragon liked this · 7 years ago
beethoventhedragon liked this · 7 years ago -
 quantum-friend-theory liked this · 7 years ago
quantum-friend-theory liked this · 7 years ago -
 forrestparrish liked this · 7 years ago
forrestparrish liked this · 7 years ago -
 circuitz42 liked this · 7 years ago
circuitz42 liked this · 7 years ago -
 santessero liked this · 7 years ago
santessero liked this · 7 years ago -
 insert-math-username reblogged this · 7 years ago
insert-math-username reblogged this · 7 years ago -
 tropicalcynicism reblogged this · 7 years ago
tropicalcynicism reblogged this · 7 years ago -
 insert-math-username reblogged this · 7 years ago
insert-math-username reblogged this · 7 years ago -
 mathematerotics reblogged this · 7 years ago
mathematerotics reblogged this · 7 years ago -
 bozonkwark reblogged this · 7 years ago
bozonkwark reblogged this · 7 years ago -
 schitzjared liked this · 7 years ago
schitzjared liked this · 7 years ago -
 languid-spring reblogged this · 7 years ago
languid-spring reblogged this · 7 years ago -
 languid-spring liked this · 7 years ago
languid-spring liked this · 7 years ago -
 guesswhowhere reblogged this · 7 years ago
guesswhowhere reblogged this · 7 years ago -
 jennybadwan97-blog liked this · 7 years ago
jennybadwan97-blog liked this · 7 years ago -
 maths-spot reblogged this · 7 years ago
maths-spot reblogged this · 7 years ago -
 hellaonpoint liked this · 7 years ago
hellaonpoint liked this · 7 years ago -
 mascmansmoke liked this · 7 years ago
mascmansmoke liked this · 7 years ago -
 flipflopfloe reblogged this · 7 years ago
flipflopfloe reblogged this · 7 years ago -
 softfawnn liked this · 7 years ago
softfawnn liked this · 7 years ago
![How To Draw A Regular Pentagon [x]](https://64.media.tumblr.com/e789070555deb967c4b2323363be07b9/tumblr_opd8xi3HCJ1vnq1cro1_500.gif)


